定义
朗伯w函数,又称欧米伽函数或乘积对数函数,是复变函数$ y=x \cdot e^x $的反函数,用$ W(x) $表示 若$ x \cdot e^x=a $,则有$ W(a)=x $ 当$ a=1 $时,$ x=W(1)=\Omega \approx 0.56714329040978387 $,这个数被称为$ \Omega $常数 $ W(x) $是一个超越函数,无法用基本初等函数来表示
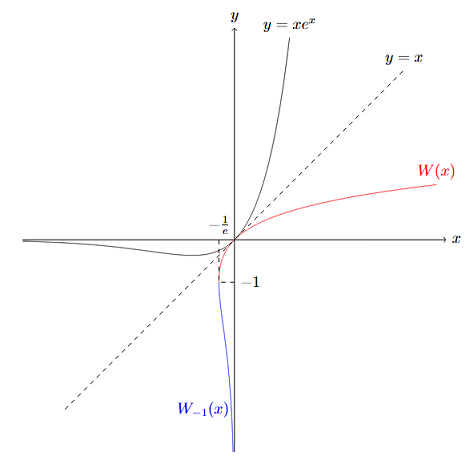
如果我们把朗伯函数的定义域限制在$ \left[\left.-\frac{1}{e},+\infty\right)\right. $,取其在$ [1,+\infty) $上的函数值,那么就定义了一个单调递增的函数$ W(x) $ 定义域限制在$ \left[\left.-\frac{1}{e},+0\right)\right. $,取其在$ (-\infty,-1) $上的函数值,那么就定义了一个单调递减的函数$ W_{-1}(x) $
应用
很多包含指数函数,或者对数函数的超越方程,可以利用朗博w函数求解,如
$ x \cdot e^x=c $
$$ x=W(c) $$$ \dfrac{x}{e^{x}}=c $
$$ \large \begin{align*} x \cdot e^{-x} &=c\\ -x \cdot e^{-x} &=-c\\ W(-x \cdot e^{-x}) &=W(-c)\\ -x &=W(-c)\\ x &=-W(-c) \end{align*} $$$ x+e^x=c $
令$ t=e^x $
$$ \large \begin{align*} \ln(t)+t &= c\\ e^{\ln(t)+t} &= e^c\\ te^t &= e^c\\ t &= W(e^c)\\ e^x &= W(e^c)\\ x &= \ln(W(e^c)) \end{align*} $$$ x-e^x=c $
令$ t=e^x $
$$ \large \begin{align*} \ln(t)-t &= c\\ e^{\ln(t)-t} &= e^c\\ te^{-t} &= e^c\\ -te^{-t} &= -e^c\\ -t &= W(-e^c)\\ -e^x &= W(-e^c)\\ x &= \ln(-W(-e^c)) \end{align*} $$$ x\ln(x)=c $
令$ t=\ln(x) $
$$ \large \begin{align*} te^t &= c\\ t &= W(c)\\ \ln(x) &= W(c)\\ x &= e^{W(c)} \end{align*} $$$ \dfrac{x}{\ln(x)}=c $
令$ t=\ln(x) $
$$ \large \begin{align*} \frac{e^t}{t} &= c\\[4mm] \frac{t}{e^t} &= \frac{1}{c}\\[4mm] te^{-t} &= \frac{1}{c}\\[4mm] -te^{-t} &= -\frac{1}{c}\\[4mm] -t &= W\left(-\frac{1}{c}\right)\\[4mm] -\ln(x) &= W\left(-\frac{1}{c}\right)\\[4mm] x &= e^{-W\left(-\frac{1}{c}\right)} \end{align*} $$$ x+\ln(x)=c $
$$ \large \begin{align*} e^{x+\ln(x)} &= e^c\\ xe^x &= e^c\\ x &= W(e^c) \end{align*} $$$ x-\ln(x)=c $
$$ \large \begin{align*} e^{x-\ln(x)} &= e^c\\ \frac{e^x}{x} &= e^c\\[4mm] \frac{x}{e^x} &= e^{-c}\\[4mm] xe^{-x} &= e^{-c}\\ -xe^{-x} &= -e^{-c}\\ -x &= W\left(-e^{-c}\right)\\ x &= -W\left(-e^{-c}\right)\\ \end{align*} $$$ ax^b+c\ln(dx)=f $
$$ \large \begin{align*} e^{ax^b+c\ln(dx)} &= e^f\\ e^{ax^b} \cdot d^cx^c &= e^f\\ \sqrt[a]{e^{ax^b} \cdot d^cx^c} &= \sqrt[a]{e^f}\\ e^{x^b} \cdot d^{\frac{c}{a}}x^{\frac{c}{a}} &= e^{\frac{f}{a}}\\ e^{x^b} \cdot x^{\frac{c}{a}} &= \frac{e^{\frac{f}{a}}}{d^{\frac{c}{a}}}\\ \end{align*} $$令$ t=x^b $
$$ \large \begin{align*} e^t \cdot t^{\frac{c}{ab}} &= \frac{e^{\frac{f}{a}}}{d^{\frac{c}{a}}}\\ \left(e^t \cdot t^{\frac{c}{ab}}\right)^{\frac{ab}{c}} &= \left(\frac{e^{\frac{f}{a}}}{d^{\frac{c}{a}}}\right)^{\frac{ab}{c}}\\ e^{t \cdot \frac{ab}{c}} \cdot t &= \left(\frac{e^f}{d^c}\right)^{\frac{b}{c}}\\ e^{t \cdot \frac{ab}{c}} \cdot t \cdot \frac{ab}{c} &= \left(\frac{e^f}{d^c}\right)^{\frac{b}{c}} \cdot \frac{ab}{c}\\ t \cdot \frac{ab}{c} &= W\left(\left(\frac{e^f}{d^c}\right)^{\frac{b}{c}} \cdot \frac{ab}{c}\right)\\ t &= \frac{c}{ab} \cdot W\left(\left(\frac{e^f}{d^c}\right)^{\frac{b}{c}} \cdot \frac{ab}{c}\right)\\ x^b &= \frac{c}{ab} \cdot W\left(\left(\frac{e^f}{d^c}\right)^{\frac{b}{c}} \cdot \frac{ab}{c}\right)\\ x &= \sqrt[b]{\frac{c}{ab} \cdot W\left(\left(\frac{e^f}{d^c}\right)^{\frac{b}{c}} \cdot \frac{ab}{c}\right)} \end{align*} $$$ x^x=c $
$$ \large \begin{align*} \ln(x^x) &= \ln(c)\\ x\ln(x) &= \ln(c) \end{align*} $$令$ t=\ln(x) $
$$ \large \begin{align*} te^t &= \ln(c)\\ t &= W(\ln(c))\\ \ln(x) &= W(\ln(c))\\ x &= e^{W(\ln(c))} \end{align*} $$$ a^x+x=c $
令$ t=a^x $
$$ \large \begin{align*} t+\log_{a}t &= c\\ a^{t+\log_{a}t} &= a^c\\ ta^t &= a^c\\ t\left(e^{\ln(a)}\right)^t &= a^c\\ te^{t\ln(a)} &= a^c\\ t\ln(a) \cdot e^{t\ln(a)} &= a^c\ln(a)\\ t\ln(a) &= W\left(a^c\ln(a)\right)\\ t &= \frac{W\left(a^c\ln(a)\right)}{\ln(a)}\\ a^x &= \frac{W\left(a^c\ln(a)\right)}{\ln(a)}\\ x &= \log_{a}\left(\frac{W\left(a^c\ln(a)\right)}{\ln(a)}\right) \end{align*} $$